Geometric Path Enumeration for Equivalence Verification of Neural Networks

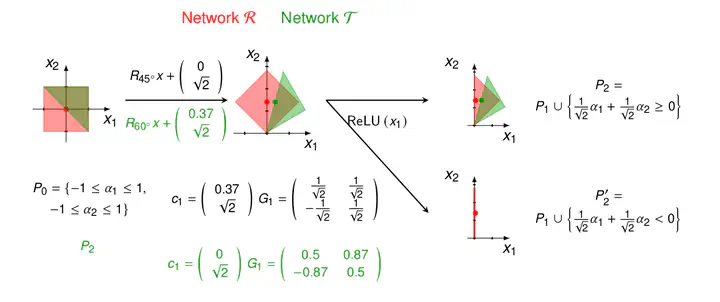
As neural networks (NNs) are increasingly introduced into safety-critical domains, there is a growing need to formally verify NNs before deployment. In this work we focus on the formal verification problem of NN equivalence which aims to prove that two NNs (e.g. an original and a compressed version) show equivalent behavior. Two approaches have been proposed for this problem: Mixed integer linear programming and interval propagation. While the first approach lacks scalability, the latter is only suitable for structurally similar NNs with small weight changes. The contribution of our paper has four parts. First, we show a theoretical result by proving that the epsilon-equivalence problem is coNP-complete. Secondly, we extend Tran et al.’s single NN geometric path enumeration algorithm to a setting with multiple NNs. In a third step, we implement the extended algorithm for equivalence verification and evaluate optimizations necessary for its practical use. Finally, we perform a comparative evaluation showing use-cases where our approach outperforms the previous state of the art, both, for equivalence verification as well as for counter-example finding.

Conference paper

2021 IEEE 33rd International Conference on Tools with Artificial Intelligence